一、-33的补码
1、8位二进制中,最高位(首位)为符号位,0表示正数,1表示负数。其余7位表示数字的真值
2、先把33转换成二进制:33D=0100001B
3、因为是负数,在最前面加上一个1,得到原码:1010 0001
4、反码:符号位不变,其余按位取反:1101 1110
5、补码:反码+1=1101 1111
二、1的十六进制补码
好的,关于1的十六进制补码,我们首先要明白补码的概念。补码是计算机中表示负数的一种方式,对于正数来说,其补码就是原码本身。那么,1作为一个正数,在十六进制中,它的表示就是01。但通常我们不会单独说一个数字的补码,而是会在一个特定的位数下来讨论,比如8位、16位等。
如果我们考虑8位的十六进制数,那么1的十六进制原码就是00000001。而补码只有在表示负数时才与原码不同,对于正数,补码就是原码。因此,在8位十六进制下,1的补码还是00000001。
总的来说,1的十六进制补码就是其本身的十六进制表示,即01或00000001(在8位十六进制下)。希望这个解释能让你满意。
三、补码范围
八位二进制正数的补码范围是0000 0000 ~ 0111 1111 即0 ~ 127,负数的补码范围是正数的原码0000 0000 ~ 0111 1111 取反加一(也可以理解为负数1000 0000 ~ 1111 1111化为反码末尾再加一)。
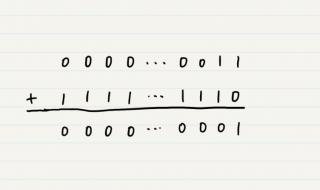
所以得到 1 0000 0000 ~ 1000 0001,1000 0001作为补码,其原码是1111 1111(-127),依次往前推,可得到-1的补码为1111 1111,那么补码0000 0000的原码是1000 0000符号位同时也可以看做数字位即表示-128,这也解释了为什么127(0111 1111)+1(0000 0001)=-128(1000 0000)。
在计算机中数据用补码表示,利用补码统一了符号位与数值位的运算,同时解决了+0、-0问题,将空出来的二进制原码1000 0000表示为-128,这也符合自身逻辑意义的完整性。因此八位二进制数表示范围为-128~+127。
四、补码怎么算
1、正数的补码表示:
正数的补码 = 原码
负数的补码 = {原码符号位不变} + {数值位按位取反后+1} or
= {原码符号位不变} + {数值位从右边数第一个1及其右边的0保持不变,左边安位取反}
以十进制整数+97和-97为例:
+97原码 = 0110_0001b
+97补码 = 0110_0001b
-97原码 = 1110_0001b
-97补码 = 1001_1111b
2、纯小数的原码:
纯小数的原码如何得到呢?方法有很多,在这里提供一种较为便于笔算的方法。
以0.64为例,通过查阅可知其原码为0.1010_0011_1101_0111b。
操作方法:
将0.64 * 2^n 得到X,其中n为预保留的小数点后位数(即认为n为小数之后的小数不重要),X为乘法结果的整数部分。
此处将n取16,得
X = 41943d = 1010_0011_1101_0111b
即0.64的二进制表示在左移了16位后为1010_0011_1101_0111b,因此可以认为0.64d = 0.1010_0011_1101_0111b 与查询结果一致。
再实验n取12,得
X = 2621d = 1010_0011_1101b 即 0.64d = 0.1010_0011_1101b,在忽略12位小数之后的位数情况下,计算结果相同。
3、纯小数的补码:
纯小数的补码遵循的规则是:在得到小数的源码后,小数点前1位表示符号,从最低(右)位起,找到第一个“1”照写,之后“见1写0,见0写1”。
以-0.64为例,其原码为1.1010_0011_1101_0111b
则补码为:1.0101_1100_0010_1001b
当然在硬件语言如verilog中二进制表示时不可能带有小数点(事实上不知道哪里可以带小数点)。
4、一般带小数的补码
一般来说这种情况下先转为整数运算比较方便
-97.64为例,经查询其原码为1110_0001.1010_0011_1101_0111b
笔算过程:
-97.64 * 2^16 = -6398935 = 1110_0001_1010_0011_1101_0111b,其中小数点在右数第16位,与查询结果一致。
则其补码为1001_1110_0101_1100_0010_1001b,在此采用 负数的补码 = {原码符号位不变} + {数值位按位取反后+1} 方法
5、补码得到原码:
方法:符号位不动,幅度值取反+1 or符号位不动,幅度值-1取反
-97.64补码 = 1001_1110(.)0101_1100_0010_1001b
取反 = 1110_0001(.)1010_0011_1101_0110b
+1 = 1110_0001(.)1010_0011_1101_0111b 与查询结果一致
6、补码的拓展:
在运算时必要时要对二进制补码进行数位拓展,此时应将符号位向前拓展。
-5补码 = 4'b1011 = 6'b11_1011
ps.原码的拓展是将符号位提到最前面,然后在拓展位上部0.
-5原码 = 4‘b’1101 = 6'b10_0101,对其求补码得6'b11_1011,与上文一致。
扩展资料:
计算机中的符号数有三种表示方法,即原码、反码和补码。三种表示方法均有符号位和数值位两部分,符号位都是用0表示“正”,用1表示“负”,而数值位,三种表示方法各不相同。
在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统一处理;同时,加法和减法也可以统一处理。此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路。
五、-19的补码是多少
1、一般是按8位二进制来做,所以-19的原码是(10010011),反码是(11101100),补码是(11101101)。
2、数据在计算机中是以二进制的形式存在的,比如bytea=6;byteb=-6
3、分为两种情况来说,一种是正数,一种是负数;对于正数6来说,原码就是00000110,反码和补码也是这个;而对于-6来说,原码就是10000110,这是为什么呢?因为最高位(最左边的)是表示符号,0表示正数,1表示负数;
4、不管是byte,short,int还是其他的数字,最高位都是用来表示符号的,所以-6的原码就是10000110,负数的反码就是符号不变,其他的取反,就是11111001;负数的补码就是在反码的基础上加1就行了,由于是二进制的,是逢2进1,所以补码就是:11111010,;



本文《-33的补码 正数的补码》希望能帮助到你!